Howmanymagicsquaresarethere

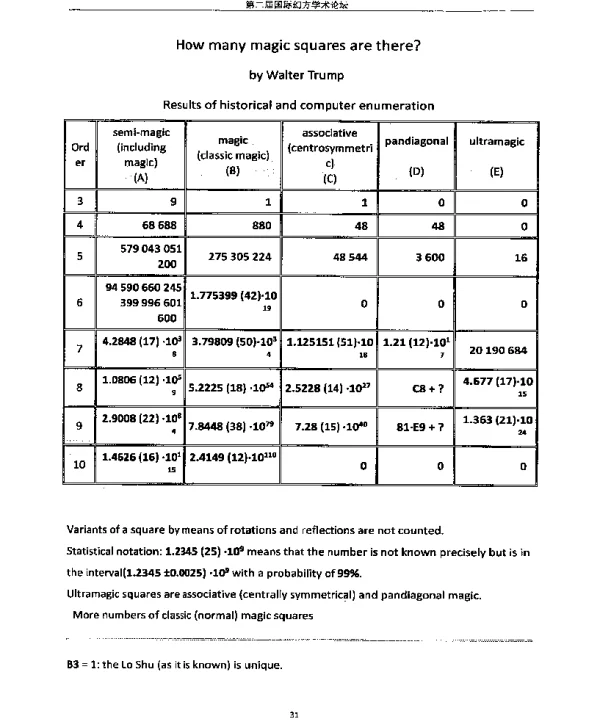
《How many magic squares are there?》是一篇探讨魔方阵数量的学术论文，该论文对数学领域中的经典问题进行了深入研究。魔方阵是一种特殊的数字排列方式，其特点是每一行、每一列以及两条对角线上的数字之和都相等。这种结构在数学、计算机科学和艺术设计中都有广泛的应用。论文通过严谨的数学方法和计算技术，分析了不同阶数的魔方阵的数量，并试图回答“有多少个魔方阵存在”这一问题。

魔方阵的概念最早可以追溯到中国古代，传说中大禹治水时出现的“洛书”，被认为是最早的三阶魔方阵。随着时间的推移，魔方阵的研究逐渐扩展到其他阶数，并成为数学家们关注的重要课题。论文首先回顾了魔方阵的历史背景，介绍了其基本定义和性质，为后续的分析奠定了基础。

论文的核心内容是关于魔方阵数量的计算。对于小阶数的魔方阵，如三阶或四阶，可以通过穷举法找到所有可能的排列方式。然而，随着阶数的增加，计算量呈指数级增长，使得传统的穷举法变得不可行。因此，作者引入了更高效的算法和数学模型，以减少计算复杂度并提高求解效率。

在分析过程中，论文讨论了魔方阵的不同类型，包括标准魔方阵、幻方矩阵、对称魔方阵等。每种类型的魔方阵都有其独特的性质和构造方法。例如，标准魔方阵要求每个数字从1到n²不重复地排列，而对称魔方阵则需要满足一定的对称性条件。这些不同的类型使得魔方阵的研究更加丰富和复杂。

为了计算魔方阵的数量，作者采用了组合数学和群论的方法。组合数学提供了计算排列组合的工具，而群论则用于分析魔方阵的对称性和变换关系。通过这些方法，论文展示了如何将复杂的魔方阵问题转化为可计算的数学模型。此外，作者还利用了计算机程序进行大规模的计算，验证了理论结果的正确性。

论文还探讨了魔方阵的生成方法。对于某些特定的阶数，如奇数阶或偶数阶，存在多种构造魔方阵的算法。例如，西门子算法适用于奇数阶魔方阵的构造，而卢卡斯算法则用于偶数阶魔方阵的生成。这些算法不仅帮助研究人员快速生成魔方阵，也为进一步研究其性质提供了便利。

在研究过程中，作者发现魔方阵的数量随着阶数的增加而迅速增长，但具体数值却难以精确计算。对于较大的阶数，如五阶或六阶，魔方阵的数量已经非常庞大，甚至超出了传统计算能力的范围。因此，论文提出了一些优化策略，以减少计算时间并提高精度。

除了计算数量外，论文还讨论了魔方阵的变体和推广形式。例如，部分魔方阵允许重复的数字，或者仅要求某些行或列的和相等。这些变体扩展了魔方阵的应用范围，并引发了更多的研究兴趣。此外，作者还提到魔方阵在密码学、游戏设计和数据加密中的潜在应用，表明其研究价值不仅限于纯数学领域。

论文最后总结了当前关于魔方阵数量的研究成果，并指出了未来研究的方向。尽管已有许多进展，但仍然有许多未解的问题，例如更高阶数的魔方阵数量仍未完全确定。作者建议进一步结合人工智能和机器学习技术，以探索魔方阵的更多可能性。

总的来说，《How many magic squares are there?》这篇论文为魔方阵的研究提供了重要的理论支持和计算方法。通过对魔方阵数量的系统分析，论文不仅加深了人们对这一数学概念的理解，也为相关领域的进一步发展奠定了基础。