基于浅水方程的LBM方柱绕流分析

《基于浅水方程的LBM方柱绕流分析》是一篇研究流体力学中复杂流动问题的论文，主要探讨了利用格子玻尔兹曼方法（Lattice Boltzmann Method, LBM）对二维方柱绕流现象进行数值模拟的方法和结果。该论文结合了浅水方程与LBM技术，旨在为工程应用中的水流模拟提供一种高效、准确的计算手段。

在流体力学领域，绕流问题一直是研究的重点之一，尤其是在水利工程、环境科学以及风能开发等领域具有广泛的应用价值。方柱作为一种常见的障碍物结构，其绕流行为对周围的流场分布、压力分布以及涡旋生成等均有显著影响。因此，对这种典型结构的绕流特性进行深入研究具有重要的理论和实际意义。

传统的数值模拟方法如有限体积法或有限元法虽然在处理复杂流动问题时表现出良好的性能，但其在计算效率和并行化方面存在一定局限性。而格子玻尔兹曼方法作为一种新兴的计算流体力学方法，因其易于并行计算、边界条件处理简单以及物理意义明确等优点，近年来得到了广泛应用。

该论文将浅水方程与LBM相结合，构建了一个适用于二维不可压缩粘性流体的数值模型。浅水方程是描述大尺度水体运动的基本方程，适用于河流、湖泊等宽浅水域的流动分析。通过引入LBM方法，作者实现了对浅水方程的离散求解，并验证了该方法在模拟方柱绕流过程中的有效性。

在论文的研究过程中，作者首先建立了方柱绕流的几何模型，并设定了合理的边界条件和初始条件。随后，采用LBM方法对流场进行了数值模拟，重点分析了不同雷诺数下方柱周围的流动结构、速度分布以及压力分布的变化情况。此外，还研究了方柱后方尾涡的形成和发展规律，以及其对整体流动的影响。

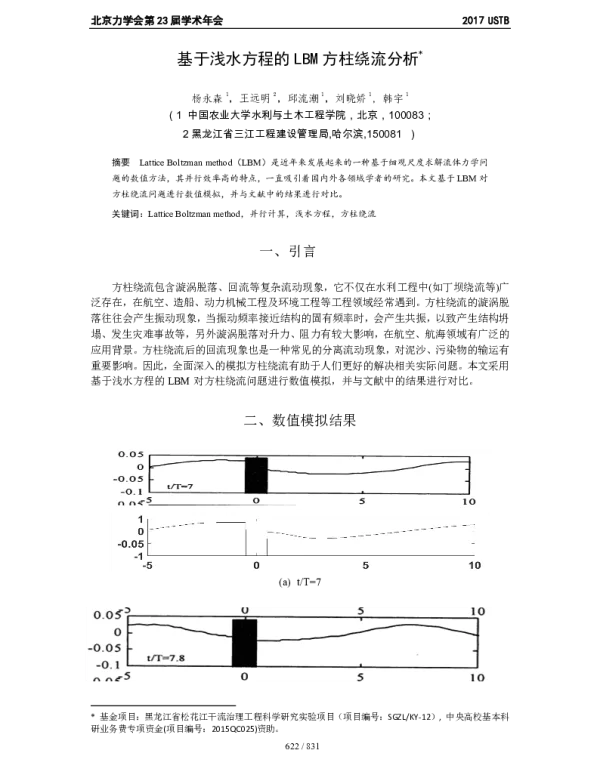
研究结果表明，基于浅水方程的LBM方法能够有效地捕捉到方柱绕流中的关键流动特征，包括分离流、回流区以及尾涡结构等。同时，该方法在计算精度和稳定性方面表现良好，能够在较短时间内完成大规模的数值模拟任务。

论文还对比了不同网格分辨率对模拟结果的影响，发现随着网格密度的增加，模拟结果逐渐趋于稳定，说明该方法具有良好的收敛性和可靠性。此外，作者还讨论了LBM方法在处理复杂边界条件时的优势，例如可以方便地处理非结构化网格和多相流问题。

通过对方柱绕流问题的深入研究，该论文不仅验证了基于浅水方程的LBM方法在工程流体力学中的适用性，也为后续相关研究提供了理论支持和技术参考。未来，该方法有望在更多复杂的流动问题中得到应用，如城市排水系统优化、海洋工程中的波浪与结构相互作用分析等。

总之，《基于浅水方程的LBM方柱绕流分析》是一篇具有较高学术价值和工程应用潜力的论文，其研究成果为计算流体力学的发展提供了新的思路和方法，同时也为相关领域的工程实践提供了有力的技术支撑。